Перейти к:
Основные принципы применения описательной статистики в медицинских исследованиях
https://doi.org/10.47093/2218-7332.2021.12.3.4-16
Аннотация
Описательная статистика - дисциплина, которая объединяет методы оценки, обобщения и представления данных. В этом руководстве авторы представляют два основных типа данных: качественные и количественные переменные, а также наиболее распространенные подходы к числовому и графическому описанию их распределений. В статье описаны два основных набора параметров: меры центральной тенденции (среднее арифметическое, медиана, мода) и вариации (стандартное отклонение, квантили), а также предложены подходы к их практическому применению. Авторы объясняют различия между генеральной совокупностью и случайными выборками, которые обычно становятся предметом научных исследований. Показатели, которые характеризуют выборку, например меры центральной тенденции, представляют точечные оценки, которые могут отличаться от соответствующих характеристик общей популяции. Руководство познакомит читателя с концепцией доверительного интервала - диапазона значений, который с определенной вероятностью содержит истинное значение соответствующего параметра общей популяции. Все представленные концепции и определения проиллюстрированы примерами, которые имитируют данные реальных медицинских исследований.
Ключевые слова
Список сокращений:
- SD – standard deviation, стандартное отклонение
- SE – standard error, стандартная ошибка
- ДИ – доверительный интервал
- ИКР – интерквартильный размах
Один из наиболее известных и влиятельных статистиков XX века Рональд Фишер писал в своей работе «О математических основах теоретической статистики» о том, что «…целью статистической обработки является сокращение объема данных. Большой объем данных …должен быть сведен к относительно небольшому числу параметров, которые адекватно описывают целое» [1]. На наш взгляд, эта цитата превосходно передает сущность описательной статистики – раздела статистики, посвященного обобщению и описанию данных, который представляет инструменты для исследования массивов данных и их представления. Медицинские исследования могут объединять данные сотен или тысяч единиц наблюдения (отдельных пациентов, животных, клеток или других объектов), которые невозможно понять, изучая их по отдельности. Однако исследователей обычно интересует ограниченное число параметров, таких как возраст или анамнез курения, которые можно обобщить и представить с использованием методов описательной статистики и таким образом получить представление обо всей выборке. Другими словами, авторы стремятся описать свойства всей выборки несколькими числами или одним графиком.
Исследование и обобщение полученных данных является первым и одним из наиболее важных этапов статистического анализа. Его целью является получение адекватного описания исследуемых переменных для лучшего понимания их особенностей. В результате исследователи определяют параметрическую модель, которая наилучшим образом отражает распределение данных. Этот этап играет ключевую роль, поскольку выбранная модель определяет дальнейшие подходы к тестированию статистических гипотез. Таким образом, основными задачами описательной статистики являются исследование данных, определение типа их распределения, выявление ошибок, а также нетипичных значений (выбросов). Описательная статистика позволяет определить долю пропущенных значений для каждой переменной и помогает оценить риск смещения. В целом адекватное и понятное представление переменных обычно свидетельствует о качественном подходе к сбору, анализу и интерпретации данных.
Целью этого руководства является представление основных методов описания различных типов переменных, а также их графического отображения.
Генеральная совокупность и случайная выборка
В медицинских исследованиях обычно анализируют данные случайной выборки пациентов из общей популяции (генеральной совокупности), например группу пациентов с инфарктом миокарда, случайным образом отобранную в одном или нескольких специализированных центрах. Однако в результате анализа этой ограниченной выборки исследователи стремятся прийти к выводам, применимым ко всей генеральной совокупности (в представленном примере – все пациенты с инфарктом миокарда в реальной практике). Каждая величина, полученная при анализе выборки, является приближенной оценкой соответствующего параметра генеральной совокупности, например среднее арифметическое какой-либо переменной в исследуемой выборке является оценкой среднего арифметического в общей популяции пациентов. Поэтому величины, рассчитанные на основании изучения случайной выборки, называют точечными оценками. Поскольку точечные оценки получают при анализе случайной выборки с некоторой долей неопределенности, все выводы, полученные таким образом, являются вероятностными суждениями. В связи с этим для лучшего понимания некоторых концепций, представленных в этом обзоре, мы рекомендуем читателям освежить в памяти основные постулаты теории вероятностей и теории множеств, которые представлены в первом руководстве этого цикла [2].
ТИПЫ ПЕРЕМЕННЫХ
В статистике переменной называют характеристику (признак), которая описывает свойства изучаемого объекта (пациента, лабораторного животного, клеточной культуры и т.д.) и может принимать различные значения (меняться или варьироваться). Выбор переменных зависит от целей исследования. Факторы риска и исходы с точки зрения статистики также являются переменными (более подробно факторы риска и исходы в исследованиях различного дизайна описаны в предыдущем руководстве цикла) [3]. Примерами переменных являются пол, возраст, концентрация биомаркера, число беременностей в анамнезе, стадия злокачественного новообразования, анамнез курения и др. Первым этапом анализа любого эксперимента является выбор переменных и оценка их шкалы измерения. Существуют два основных типа данных: количественные и качественные (рис. 1).

FIG. 1. Types of variables.
РИС. 1. Типы переменных.
Количественные переменные можно измерить в числовом выражении, а их величину можно представить с помощью метрической шкалы. Например, их количество можно посчитать или измерить в метрах, килограммах, ммоль/л или других единицах. Среди количественных переменных выделяют непрерывные и дискретные.
Непрерывные переменные могут принимать бесконечное число значений в промежутке между двумя любыми значениями, включая целые числа и доли. Примерами могут служить масса тела, концентрация билирубина или температура.
Дискретные переменные могут принимать ограниченное число значений, которые обычно представлены целыми числами. Например, число обострений заболевания и количество клеток в поле зрения микроскопа являются дискретными величинами.
Качественные переменные (категориальные) невозможно измерить, вместо этого их разделяют на группы (категории). Например, цвет волос нельзя измерить по метрической шкале, однако можно выделить несколько групп (категорий) этого признака: темные волосы, светлые, рыжие и т.д. Качественные переменные разделяют на порядковые (ординарные) и номинальные.
Порядковые переменные могут быть ранжированы в соответствии со своим рангом. В частности, стадия опухолевого процесса не измеряется по метрической шкале, хотя более высокие значения характеризуют более тяжелое течение (поздние стадии) заболевания.
Номинальные переменные не могут быть ранжированы, как, например, место жительства, профессия и некоторые другие признаки. Одним из наиболее распространенных типов номинальных переменных являются бинарные (дихотомические) переменные, которые могут принимать только два значения (исход наступил или нет, пациент выжил или умер, мужской пол или женский).
В статистике выделяют и другие классы переменных, которые не представлены в этом обзоре. Дополнительную информацию о них можно узнать в книгах по биомедицинской статистике [4].
ОБОБЩЕНИЕ НЕПРЕРЫВНЫХ ДАННЫХ
Распределение данных и гистограммы
Как уже было сказано, целью описательной статистики является описание данных, полученных при исследовании случайной выборки пациентов (или иных наблюдений). Каждый параметр может принимать различные значения, и исследователей обычно интересует вероятность каждого возможного исхода.
На первом этапе можно осуществить визуализацию распределения переменной. Для этого необходимо выстроить все полученные значения переменной в порядке возрастания и разделить их на небольшие группы с одинаковыми интервалами, которые называют разрядами. Затем производят подсчет, какое количество наблюдаемых значений переменной попадает в каждый разряд. Графическое изображение этого метода называют гистограммой. Ширина и количество разрядов зависит от диапазона значений переменной, которые сгруппированы в каждый разряд. Чем меньше интервал значений, тем уже столбики, изображающие разряды.
В качестве примера рассмотрим значения концентрации креатинина в сыворотке крови, измеренной в мкмоль/л, в случайной выборке из 20 пациентов. Полученные результаты представлены в порядке от наименьшего к наибольшему: 133,5; 133,8; 138,0; 138,2; 139,3; 142,2; 143,1; 144,1; 145,0; 149,0; 149,1; 149,3; 151,0; 151,9; 152,5; 152,8; 153,4; 153,8; 158,7; 158,9.
Каждый столбик на гистограмме, представленной на рисунке 2, отображает разряд (небольшой диапазон концентраций креатинина, отложенный на оси X). Высота каждого столбика отражает число пациентов, у которых концентрация креатинина попадает в соответствующий интервал значений (ось Y). Таким образом, у двух пациентов концентрация креатинина в сыворотке находится в интервале от 130 до 134,9 мкмоль/л, у трех – в интервале от 135 до 139,9 мкмоль/л, у трех – в интервале от 140 до 144,9 мкмоль/л и т.д.
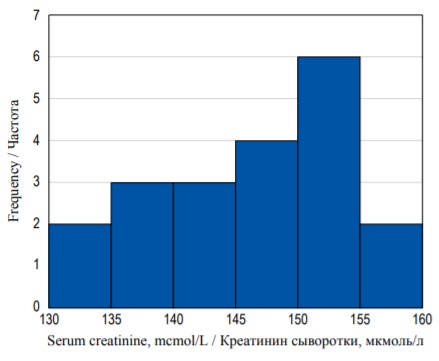
FIG. 2. Frequency histogram of serum creatinine concentration distribution.
РИС. 2. Гистограмма распределения частот концентрации креатинина.
Нередко исследователи стремятся оценить вероятность того, что концентрация креатинина у пациента попадет в определенный диапазон. Однако гистограмма распределения частот демонстрирует распространенность каждого исхода, но не его вероятность. Для оценки вероятности необходимо определить распределение плотности вероятностей. Для этого нормализуют гистограмму, разделив количество исходов в каждом разряде на число наблюдений, умноженное на ширину каждого разряда. Получившийся график называют гистограммой плотности распределения вероятности (рис. 3). Форма гистограммы при этом не меняется, однако теперь она отображает плотность распределения вероятностей, а площадь каждого столбика (разряда) соответствует вероятности некоего события (в рассматриваемом примере вероятность того, что концентрация креатинина попадет в указанный интервал значений). В свою очередь, площадь всей гистограммы равна 1,0 (100%), поскольку она равна сумме вероятностей всех возможных исходов в пространстве элементарных событий. Следует помнить, что значения на оси Y не отражают вероятности исходов, для оценки которой необходимо определять площадь элементов гистограммы.
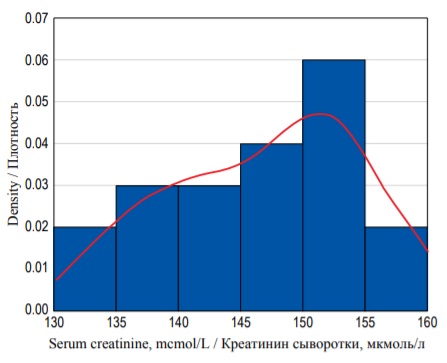
FIG. 3. Density histogram of the serum creatinine concentration with a probability density function (red curve).
РИС. 3. Гистограмма распределения плотности вероятностей концентрации креатинина сыворотки с функцией плотности вероятностей (красная кривая).
Площадь всей гистограммы равна сумме площадей всех разрядов. Поскольку ширина каждого разряда (столбика) равна 5, а высоту можно оценить по значениям на оси Y, мы можем вычислить площадь всей гистограммы, чтобы проверить вышесказанные утверждения:
S = (0,02×5) + (0,03×5) + (0,03×5) + (0,04×5) + (0,06×5) + (0,02×5) = 1,0.
Площадь действительно равна 1,0 (или 100%). Сходным образом можно вычислить вероятность каждого возможного события, то есть попадания концентрации креатинина в определенный диапазон значений. Например, вероятность выявления концентрации креатинина в интервале от 130 до 134,9 мкмоль/л равна (0,02×5) = 0,1 (или 10%). Точно так же можно определить вероятность выявления концентрации креатинина менее 145 мкмоль/л. Для этого необходимо суммировать площади разрядов от наименьшего значения до 144,9:
(0,02×5) + (0,03×5) + (0,03×5) = 0,4 (или 40%).
В представленном примере описаны 20 индивидуальных наблюдений, однако в клинических исследованиях ученые нередко анализируют очень большие массивы непрерывных переменных. В больших выборках интервалы для каждого разряда обычно существенно меньше, в связи с чем гистограмма становится сглаженной и своей формой начинает напоминать кривую (рис. 4). Площадь под кривой можно определить путем вычисления определенного интеграла, пределами которого являются два значения переменной на оси X, и эта величина будет равна вероятности того, что индивидуальное наблюдение попадет в выбранный диапазон значений. Как следствие, чем меньший интервал значений мы выбираем, тем меньше вероятность того, что значение переменной в него попадет, поскольку соответствующая площадь под кривой будет меньше.
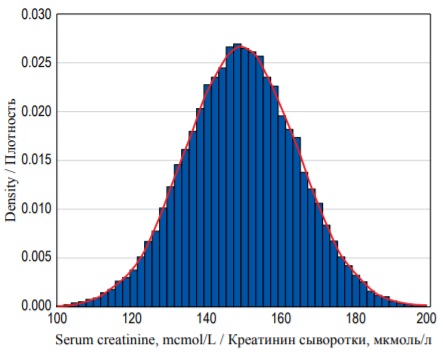
FIG. 4. Probability density distribution for 25 000 random observations of serum creatinine concentration with a probability density function (red curve).
РИС. 4. Распределение плотности вероятностей для 25 000 случайных измерений концентрации креатинина сыворотки с функцией плотности вероятностей (красная кривая).
Числовое описание распределения непрерывной переменной
Гистограмма графически представляет распределение, однако ему можно дать и числовую характеристику. Существует набор параметров, которые описывают пороговые значения распределения.
Квантили – это значения переменной, которые разделяют весь диапазон значений (вероятность) на равные интервалы. В представленном выше примере 10% (0,1) значений концентрации креатинина располагаются в диапазоне менее 135 мкмоль/л, иными словами, вероятность того, что значение концентрации будет менее 135 мкмоль/л, составляет 10%. Таким образом, 135 является 0,1 (10%) квантилем. В том же примере 145 является 0,4 (40%) квантилем.
Некоторые квантили имеют специальные названия в зависимости от количества интервалов значений переменной, которые они создают. Наиболее распространенным типом квантилей являются перцентили или процентили (100 интервалов, или вероятность, представленная в процентах). Процентили нередко используют в популяционных исследованиях в области медицины. Например, фраза «90-й процентиль массы тела трехлетних мальчиков равен 17,41 кг» означает, что 90% трехлетних мальчиков весят менее 17,41 кг.
Другим распространенным вариантом квантилей являются квартили, которые делят распределение на четыре равных интервала. Квантиль, соответствующий значению 0,25 (25-й процентиль), отделяет 25% значений, его называют первым квартилем (Q1). Квантиль, соответствующий значению 0,5 (или 50-й процентиль), называют медианой (или вторым квартилем, Q2); он делит распределение на два равных интервала. По определению половина (50%) всех значений в распределении меньше медианы, а половина – больше. Третьим квартилем (Q3) называют 0,75 квантиль (75-й процентиль). В представленном примере с концентрацией креатинина первый квартиль равен 141,5 мкмоль/л, медиана – 149,1 мкмоль/л, а верхний (третий) квартиль – 152,6 мкмоль/л.
Меры центральной тенденции и вариации
Существуют несколько параметров, которые описывают распределение непрерывной переменной, одни из них являются мерами центральной тенденции, другие – мерами вариации. Центральная тенденция (мера центральной тенденции) является наиболее типичным значением переменной в распределении. Наиболее часто используемыми мерами центральной тенденции являются медиана, среднее арифметическое и мода.
Среднее арифметическое (обозначается μ для генеральной совокупности и x– для выборки) рассчитывается как сумма всех значений переменной в исследуемом множестве, деленная на их количество (n):
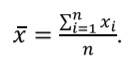
Среднее арифметическое – неоптимальный параметр для описания асимметричных распределений, поскольку на его значение могут оказывать существенное влияние выбросы (очень большие или очень маленькие значения). В приведенном примере среднее арифметическое концентрации креатинина в выборке равно 146,9 мкмоль/л.
Медиана (x˜) – это 0,5 квантиль, свойства которого были описаны в предыдущем разделе. В отличие от среднего арифметического значение медианы существенно не меняется при наличии нескольких, даже очень больших выбросов (иными словами, медиана менее чувствительна к выбросам). Если количество наблюдений нечетное, медиана рассчитывается по следующей формуле:
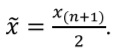
Если количество наблюдений четное, то используют следующую формулу:

Медиана – очень удобный параметр, поскольку ее можно использовать для описания различных типов распределений данных, а не только нормального.
Мода – наиболее часто встречающееся значение исследуемой переменной, которому соответствует абсолютный максимум распределения – наивысшая точка на гистограмме.
Медиана, среднее арифметическое и мода – разные параметры, которые принимают отличные друг от друга значения в большинстве распределений. Однако в некоторых симметричных распределениях, включая нормальное, их значения равны (рис. 5B). Нормальное распределение (гауссово) – распределение вероятностей, которое имеет форму симметричной кривой в виде колокола, то есть чем ближе значение переменной к среднему арифметическому, тем чаще оно встречается.
В реальной практике большинство распределений отличаются от нормального. Дополнительными параметрами, которые отражают свойства распределения, являются коэффициент асимметрии и коэффициент эксцесса (мера отношения веса хвостов распределения к его центру). При положительном коэффициенте асимметрии большая часть значений переменной сгруппирована у левого хвоста распределения, а правый хвост длиннее (рис. 5А). При отрицательном коэффициенте асимметрии, наоборот, большая часть значений сгруппирована у правого хвоста, а левый хвост длиннее (рис. 5C).
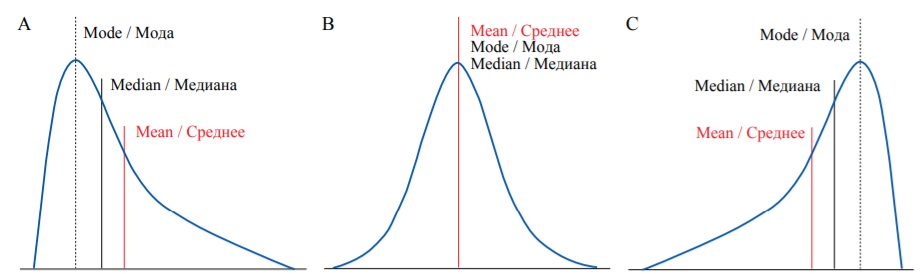
FIG. 5. Different types of probability distribution: А – Positive skew. В – Zero skew (symmetrical distribution). С – Negative skew.
РИС. 5. Различные типы распределения вероятностей: А – Положительный коэффициент асимметрии. В – Коэффициент асимметрии равен нулю (симметричное распределение). С – Отрицательный коэффициент асимметрии.
Коэффициент эксцесса отражает форму хвостов распределения (рис. 6). При отрицательном коэффициенте эксцесса (платикуртические, плосковершинные распределения) форма распределения становится более плоской, а его хвосты – короче («легче»), поскольку меньшее число значений располагается в хвостах. При положительном коэффициенте эксцесса (лептокуртические, островершинные распределения) форма распределения становится более острой, а его хвосты – длиннее («тяжелее»), поскольку большая доля значений переменной располагается в хвостах распределения. Нормальные распределения являются мезокуртическими и не имеют выраженной асимметрии.
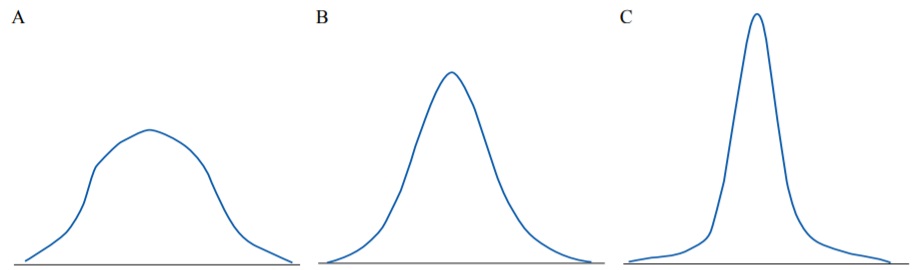
FIG. 6. Distributions with different kurtosis: А – Platykurtic (negative kurtosis). В – Mesokurtic (zero kurtosis). С – Leptokurtic (positive kurtosis).
РИС. 6. Распределения с различными коэффициентами эксцесса: А – Платикуртическое распределение (отрицательный коэффициент эксцесса). В – Мезокуртическое распределение (коэффициент эксцесса равен нулю). С – Лептокуртическое распределение (положительный коэффициент эксцесса).
К параметрам, которые описывают вариацию признаков (разброс данных), относят размах, интерквартильный размах, дисперсию и среднеквадратическое (стандартное) отклонение.
Минимум и максимум являются, соответственно, наименьшим и наибольшим значениями переменной в исследуемой выборке. В представленном примере с концентрацией креатинина наименьшее значение равно 133,5 мкмоль/л, а наибольшее – 158,9 мкмоль/л. Размах равен разнице между наибольшим и наименьшим значениями. Однако этот параметр не дает представления о распределении данных между наибольшим и наименьшим значениями. Кроме того, размах может принимать очень большие значения в выборках, содержащих выбросы. Поэтому для адекватной оценки распределения переменной требуются дополнительные параметры.
Дисперсия и среднеквадратическое (стандартное) отклонение входят в число наиболее часто используемых параметров оценки вариации признака. Бóльшая часть индивидуальных значений переменной отличается от среднего арифметического. Чем ближе значения к величине среднего арифметического, тем меньше их отклонения, и наоборот. Отклонения индивидуальных значений, превышающих среднее арифметическое, принимают положительные значения, а отклонения значений, которые меньше среднего арифметического, принимают отрицательные значения. Таким образом, вычисление среднего арифметического отклонений является бессмысленным, поскольку оно равно нулю. Вместо этого используют параметр дисперсии, который равен сумме квадратов отклонений, деленной на число наблюдений минус единица (показатель в знаменателе называют степенями свободы):
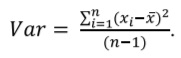
Однако использование параметра дисперсии непрактично, поскольку единицы его измерения возведены в квадрат, например дисперсия роста, измеренного в метрах, выражается в квадратных метрах. Поэтому для описания вариации данных используют среднеквадратическое отклонение или стандартное отклонение (обозначается σ для генеральной совокупности и SD [standard deviation] для выборки), которая равна квадратному корню из дисперсии:
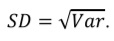
Следует помнить, что SD измеряют в тех же единицах, что и изучаемую переменную и ее среднее арифметическое. Поэтом во многих исследованиях данные представляют в виде среднего арифметического ± SD с указанием соответствующих единиц измерения, например «средняя концентрация креатинина была равна 146,9 ± 7,6 мкмоль/л». Однако в распределениях, отличающихся от нормального, значения среднего арифметического и SD могут быть обманчивыми и нелогичными, в связи с чем для описания их вариации лучше подходят медиана и интерквартильный размах (ИКР). В нормальных распределениях 68,27% всех данных (значений переменной) локализуются в пределах среднеквадратичного отклонения от среднего арифметического, 95,45% (что почти идентично 95% доверительному интервалу [ДИ], о котором написано в следующем разделе) – в пределах двух SD от среднего арифметического, а 99,73% – в пределах трех SD от среднего арифметического.
ИКР представляет собой разницу между первым и третьим квартилями, которые описаны в предшествующем разделе. ИКР дает представление о разбросе средних 50% данных. Этот показатель менее чувствителен к размеру выборки и мало зависит от наличия выбросов.
Диаграмма размаха («ящик с усами»)
Квартили, включая медиану, а также наибольшее и наименьшее значения переменной можно изобразить с помощью диаграммы размаха («ящичковая диаграмма», «ящик с усами», «бокс-плот»). На рисунке 7А представлена диаграмма частот, а также диаграмма размаха для одного и того же набора данных (см. пример с концентрацией креатинина). На диаграмме полужирная линия в середине прямоугольника изображает медиану, края прямоугольника – первый и третий квартили, а отрезки («усы») – максимальное и минимальное значения (рис. 7B).
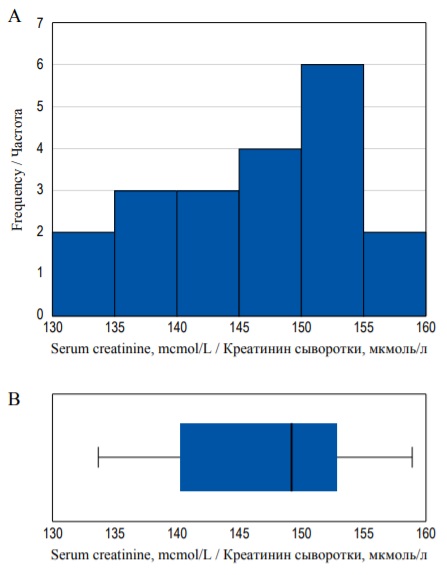
FIG. 7. Histogram (А) and box-plot (В) demonstrating the same distribution.
РИС. 7. Гистограмма (А) и диаграмма размаха (В), иллюстрирующие одно и то же распределение.
Однако в некоторых случаях «усы» могут изображать значение, равное 1,5 × ИКР выше третьего квартиля и 1,5 × ИКР ниже первого квартиля, а все значения переменной, не попавшие в этот диапазон, обозначаются как выбросы. Выбросами называют значения переменной, которые существенно отличаются от остальных наблюдений (рис. 8). Обычно их изображают в виде отдельных точек на графике. Диаграммы размаха в ряде случаев могут быть более удобны, чем гистограммы, особенно в случаях, когда необходимо сопоставить значение непрерывной переменной в нескольких подгруппах, поскольку на одном графике можно изобразить несколько диаграмм размаха (рис. 8).
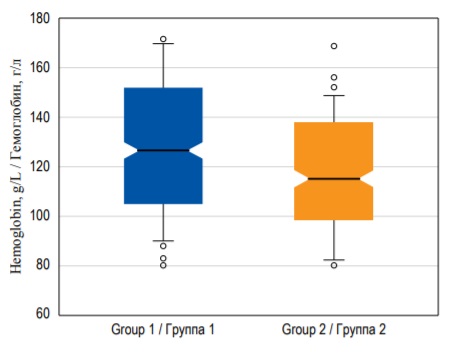
FIG. 8. Box-plots demonstrating hemoglobin median with 95% confidence interval, interquartile range, and outliers in two groups of patients.
РИС. 8. Диаграммы размаха, изображающие медиану концентрации гемоглобина c 95% доверительным интервалом, интерквартильный размах и выбросы в двух группах пациентов.
Доверительный интервал
В отличие от среднего арифметического выборки, которое является точечной оценкой среднего арифметического генеральной популяции, ДИ является интервальной оценкой, которая отражает диапазон возможных значений. 95% ДИ включает в себя 95% значений выборки и занимает интервал от 0,025 до 0,975 квантилей. В некоторых источниках ДИ называют диапазоном значений, в котором с вероятностью 95% находится истинное значение среднего арифметического генеральной совокупности. Однако более точное, хотя и более комплексное определение, следует сформулировать следующим образом: «при уровне доверия 95%, если сбор и анализ данных будут повторяться много раз, ДИ должен включать истинное значение оценки в 95% случаев». Следовательно, при расчете 95% ДИ на основании анализа 100 случайных выборок из генеральной совокупности 95% полученных ДИ будут включать истинное значение среднего арифметического генеральной совокупности (μ) [5]. Таким образом, ДИ отражает вероятность возможной случайной ошибки выборки. Однако достоверно установить истинное значение исследуемого параметра в генеральной совокупности невозможно (за исключением ситуаций, предусматривающих искусственную генерацию данных для комплексных симуляций). В связи с этим невозможно достоверно установить, попадает ли истинное значение параметра в ДИ. Величина ДИ зависит от размера выборки. В целом чем больше размер выборки, тем меньше ДИ, и наоборот. В некоторых исследованиях рассчитывают 99% ДИ, расположенный между 0,005 и 0,995 квантилями; в других – 90% ДИ. Чем шире ДИ, тем больше шансов, что он содержит истинное значение параметра [6].
ДИ можно рассчитать почти для любой точечной оценки, включая медиану, моду, отношение и т.д. Например, на рисунке 8 представлены диаграммы размаха, на которых «вырезы» вокруг медианы обозначают 95% ДИ медианы.
Стандартная ошибка (SE, standard error) отражает отклонение точечной оценки в выборке от истинного значения параметра в генеральной совокупности. Чем больше размер выборки и чем меньше величина среднеквадратического отклонения, тем меньше величина SE. Очень большие значения SE могут свидетельствовать о наличии смещения, что мешает сделать корректные выводы. В реальной практике истинные значения параметров генеральной совокупности обычно неизвестны, поэтому SE рассчитывают на основании точечных оценок выборки.
Следует отметить, что расчет ДИ обычно требуется для проверки гипотез, поэтому его значения необходимо представлять для переменных, описывающих размер эффекта в клинических исследованиях. В то же время эти параметры не всегда нужны для описания исходных характеристик выборки в публикациях.
ЧИСЛОВОЕ И ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КАЧЕСТВЕННЫХ ПЕРЕМЕННЫХ
Традиционно качественные переменные представляют в виде абсолютных значений и частот (%). Если число категорий каждого признака больше двух, то эти показатели представляют для каждой категории. Например, «среди 95 пациентов, получавших заместительную почечную терапию, 72 (76%) получали лечение гемодиализом, 20 (21%) – перитонеальным диализом, и троим (3%) была выполнена трансплантация почки». Если данные по каким-то пациентам отсутствуют, это тоже необходимо указать.
Другим возможным способом представления бинарных исходов являются шансы. Шанс равен отношению вероятности наступления исхода к вероятности того, что исход не наступит. Предположим, что в группе из 100 пациентов у 20 развился инфаркт миокарда, а у 80 – нет. Вероятность (p) развития инфаркта равна 20/100 = 0,2. Вероятность того, что инфаркт не случится, равна (1 – 0,2) = 0,8. В соответствии с определением шансы рассчитываются по формуле:
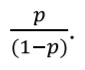
Таким образом, шансы развития инфаркта миокарда равны 0,2/0,8 = 0,25 или «1 к 4». Другими словами, среди каждых пяти пациентов у одного разовьется инфаркт миокарда, а у четырех – нет. Шансы как таковые практически не применяют для описания переменных, но они используются для расчета отношения шансов – важного метода оценки взаимосвязи между двумя бинарными переменными, например между наличием фактора риска (или его отсутствием) и наступлением исхода (подробнее об этом в предыдущем руководстве) [3].
ДИ можно рассчитать и для биноминального распределения (распределения бинарной переменной). 95% ДИ для пропорции отражает 95% вероятность того, что этот диапазон содержит истинное значение параметра генеральной совокупности (а точнее, что из 100 случайных выборок, сформированных из одной совокупности, 95 ДИ будут включать истинное значение параметра). Существует несколько методик расчета 95% ДИ для пропорции (методы Клоппера – Пирсона, Вальда, модифицированный метод Вальда), которые можно выполнить в большинстве статистических программ.
Для изображения качественных переменных можно использовать разные виды диаграмм, например столбиковую диаграмму. В столбиковой диаграмме каждый столбик отражает частоту встречаемости каждой категории исследуемого признака в виде абсолютных значений или процентов (рис. 9A). В отличие от гистограммы, в столбиковой диаграмме есть промежутки между элементами, изображающими категории, а для оценки вероятности исхода не требуется вычислять площадь фигуры. Другим методом визуализации качественных переменных является круговая диаграмма, где весь круг представляет 100% всех данных, а отдельные сегменты – различные категории признака (рис. 9B).
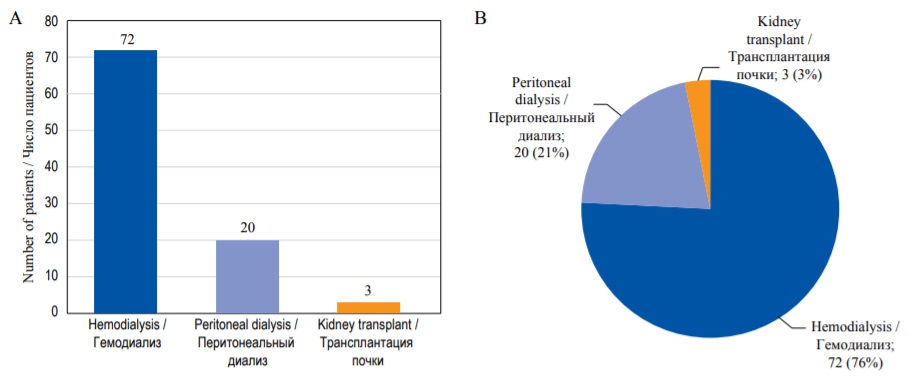
FIG. 9. Graphical representation of the qualitative data. А – Bar diagram. В – Pie diagram.
РИС. 9. Графическое представление количественных данных. А – Столбиковая диаграмма. В – Круговая диаграмма.
В некоторых случаях целесообразна трансформация количественных переменных в качественные с целью представления доли пациентов, у которых значения количественной переменной попадают в различные диапазоны. Например, для описания скорости клубочковой фильтрации в группе пациентов с заболеваниями почек можно представить не только среднее арифметическое и среднеквадратическое отклонение, но и разделить диапазон значений на категории, которые имеют практическое значение, например <15 мл/мин, 15–59,9 мл/мин и ≥60 мл/мин. Затем можно представить долю пациентов, которые попадают в каждую категорию.
КАК РАССЧИТЫВАТЬ И ПРЕДСТАВЛЯТЬ ОПИСАТЕЛЬНУЮ СТАТИСТИКУ
Каждый исследователь должен понимать суть различных параметров, описывающих распределения данных, а также методы их вычисления, однако проведение анализа данных «вручную» представляется нерациональным. Мы рекомендуем использовать специализированные приложения, такие как SPSS, Stata, R и другие, для всех видов анализа данных. При этом чтобы получить адекватные данные и корректно их представить, необходимо принять во внимание несколько аспектов.
Одним из наиболее важных моментов, которые часто недооценивают аспиранты, является кодирование переменных. Дело в том, что все статистические программы оперируют числами, поэтому базы данных должны содержать только переменные, представленные в виде числовых значений для каждого наблюдения. Это несложно сделать при работе с количественными переменными – достаточно внести полученные значения с использованием единой метрической шкалы для всех наблюдений. Например, рост пациента должен быть зафиксирован или в метрах, или в сантиметрах для всех пациентов, но нельзя попеременно использовать обе единицы измерения. Если данные представлены в разных единицах измерения, необходимо привести их к единообразию до начала любых других вычислений. Всем категориям качественных переменных должны быть присвоены однотипные числовые коды, например «0», если пациент выжил, и «1», если пациент умер.
При описании количественных переменных следует сначала подумать о том, какие параметры наилучшим образом характеризуют исследуемую выборку. Среднее арифметическое со среднеквадратическим отклонением, 95% ДИ, медиану и интерквартильный размах можно вычислить для большинства распределений, но некоторые из этих параметров могут быть менее подходящими (хотя и математически корректными). На начальном этапе анализа данных можно (и даже нужно) вычислить все эти параметры, однако в публикации обычно представляют лишь один набор параметров. Традиционно рекомендуют использовать среднее арифметическое ± SD (иногда с указанием наименьшего и наибольшего значений в скобках) для описания нормальных распределений. Для распределений, отличающихся от нормального, более информативным будет представление медианы и первого и третьего квартилей (в скобках). В некоторых случаях использование среднего арифметического и среднеквадратического отклонения для описания ненормально распределенной переменной может запутать читателя. Например, величина SD может превышать значение среднего арифметического: «срок динамического наблюдения после оперативного вмешательства составил в среднем 11,8 ± 12,1 дня». Может сложиться впечатление, что в некоторых случаях время наблюдения принимает отрицательные значения, что невозможно в реальном мире. На самом деле эти параметры могли быть рассчитаны верно, однако их использовали для описания переменной, распределение которой отличается от нормального. В подобных случаях для описания данных более предпочтительно использовать медиану и ИКР: «медиана срока динамического наблюдения после оперативного вмешательства составила 8 [ 5; 19 ] дней».
Таким образом, крайне важное значение имеет оценка типа распределения данных. Существующая классификация распределений достаточно сложна, однако при работе с количественными переменными в первую очередь имеет смысл оценить, является оно нормальным или нет. Для проверки этой гипотезы существует несколько графических и вычислительных методов (так называемых критериев нормальности): критерии (тесты) Шапиро – Уилка, Колмогорова – Смирнова, критерий Лиллиефорса (модификация теста Колмогорова – Смирнова), Андерсона – Дарлинга, графики квантиль-квантиль (К-К или Q-Q) и некоторые другие [7]. Мы не рассматриваем критерии нормальности в деталях, поскольку эта проблема входит в раздел аналитической статистики, касающейся тестирования гипотез. Одним из наиболее часто применяемых критериев нормальности, обладающим высокой мощностью, является критерий Шапиро – Уилка, который можно вычислить в любой современной статистической программе [8]. Некоторые исследователи считают этот критерий лучшим методом проверки гипотезы о нормальности распределения.
Используемый критерий нормальности и параметры, используемые для описания данных, должны быть подробно описаны в разделе «Материалы и методы» в каждой публикации. При представлении как количественных, так и качественных данных необходимо указывать общее число наблюдений в выборке и в каждой подгруппе.
При создании гистограмм необходимо выбрать подходящие число и ширину разрядов. В литературе описано несколько возможных подходов к решению этого вопроса: так называемые, правила Стерджеса, Скотта, Фридмана и Диакониса и другие [9]. Некоторые авторы предлагают выбирать число разрядов, равное квадратному корню из общего числа наблюдений [10].
Описательную статистику часто представляют в таблицах, где каждый ряд соответствует отдельной переменной, а каждая колонка – группе пациентов (табл.). Первая колонка содержит названия переменных и единицы измерения. Общее число наблюдений (пациентов) в каждой группе указывают в заголовке столбца. Чтобы представить распределение данных графически в нескольких группах, можно представить диаграммы размаха. Следует отметить, что разные статистические программы могут использовать различные подходы к вычислению квартилей, в связи с чем значения, как и графические изображения, могут немного отличаться при анализе одних и тех же данных в разных приложениях [11].
Таблица. Пример представления характеристик исследуемых групп пациентов
Table. Example of characteristics of the studied groups of patients
Группа 1 / Group 1 n = 129 | Группа 2 / Group 2 n = 131 | |
Мужской пол / Male sex, n (%) | 74 (57,4) | 68 (51,9) |
Гемоглобин, г/л / Hemoglobin, g/L | 132 ± 19 | 128 ± 17 |
Креатинин сыворотки / мкмоль/л / Serum creatinine, mcmol/L | 201,1 [ 118,4; 378,5] | 231,9 [ 126,7; 344,6] |
Примечание: качественная номинальная переменная (мужской пол) представлена в абсолютных значениях и частотах (%). Количественные переменные представлены либо как среднее ± стандартное отклонение для нормально распределенных данных, либо как медиана [Q1, Q3] для ненормально распределенных данных в обеих группах.
Note: qualitative nominal variable (male sex) is provided in absolute numbers and frequencies. Quantitative variables are given either as mean ± SD for normally distributed data or as median [Q1, Q3] for non-normally distributed data in both groups.
В этом руководстве представлены только базовые принципы описательной статистики. Более подробно с этой темой можно познакомиться в профильных руководствах [4][6].
ЗАКЛЮЧЕНИЕ
Подобно тому, как описательные исследования обеспечивают основу для формулирования гипотез и планирования дальнейших исследований, описательная статистика помогает понять полученные данные и обеспечивает базис для их дальнейшего анализа. Каждый студент медицинского вуза, аспирант, врач и исследователь должен уметь интерпретировать и вычислять основные статистические параметры, для того чтобы понимать взаимосвязь данных, полученных в случайной выборке, с общепопуляционными, критически оценивать публикуемые данные и представлять результаты своих собственных исследований должным образом.
Список литературы
1. Fisher R.A. On the mathematical foundations of theoretical statistics. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character. 1922. Vol. 222. P. 309-368. https://doi.org/10.1098/rsta.1922.0009
2. Bulanov N.M., Blyuss O.B., Munblit D.B., et al. Venn diagrams and probability in clinical research. Sechenov Med J. 2020; 11(4): 5-14. https://doi.org/10.47093/2218-7332.2020.nA5-14
3. Bulanov N.M., Blyuss O.B., Munblit D.B., et al. Studies and research design in medicine. Sechenov Med J. 2021; 12(1): 4-17. https://doi.org/10.47093/2218-7332.2021.12.1A17
4. Kirkwood B., Stern J. Essential Medical Statistics. 2nd ed. Blackwell Publishing; 2003; 512 p. ISBN: 978-0-865-42871-3.
5. RothmanK. Random error and the role of statistics. Epidemiology: An Introduction. 2nd ed. Oxford University Press; 2012: 148-163. ISBN: 9780199754557.
6. MotulskyH. Intuitive Biostatistics. 4th ed. Oxford University Press; 2018; 568 p. ISBN-13: 978-0190643560. ISBN-10: 0190643560ъ.
7. Ghasemi A., Zahediasl S. Normality tests for statistical analysis: a guide for non-statisticians. Int J Endocrinol Metab. 2012 Spring; 10(2): 486-489. https://doi.org/10.5812/ijem.3505. Epub 2012 Apr 20. PMID: 23843808. PMCID: PMC3693611
8. Mohd Razali N.M., Wah Y.B. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J Stat Model Anal. 2011; 2: 21-33.
9. Nuzzo R.L. Histograms: A useful data analysis visualization. PM R. 2019 Mar; 11(3): 309-312. https://doi.org/10.1002/pmrj.12145. Epub 2019 Mar 7. PMID: 30761760
10. Spriestersbach A., Rohrig B., Prel J.B., et al. Descriptive Statistics: The specification of statistical measures and their presentation in tables and graphs - Part 7 of a series on evaluation of scientific publications. Dtsch Arztebl. 2009; 106(36): 578-583. https://doi.org/10.3238/arztebl.2009.0578
11. Langford E. Quartiles in elementary statistics. Journal of Statistics Education. 2017; 14(3). https://doi.org/10.1080/10691898.2006.!1910589
Об авторах
Н. М. БулановРоссия
Буланов Николай Михайлович - кандидат медицинских наук, доцент кафедры внутренних, профессиональных болезней и ревматологии ФГАОУ ВО «Первый МГМУ им. И.М. Сеченова» Минздрава России (Сеченовский Университет).
Ул. Трубецкая, д. 8, стр. 2, г. Москва, 119991, Тел.: +7 (919) 100-22-79
А. Ю. Суворов
Россия
Суворов Александр Юрьевич - кандидат медицинских наук, главный статистик Центра анализа сложных систем.
Ул. Трубецкая, д. 8, стр. 2, Москва, 119991
О. Б. Блюсс
Россия
Блюсс Олег Борисович - кандидат физико-математических наук, доцент кафедры педиатрии и детских инфекционных болезней Первый МГМУ им. И.М. Сеченова; старший преподаватель Школы физики, астрономии и математики Университета Хартфордшира.
Ул. Трубецкая, д. 8, стр. 2, Москва, 119991; Хатфилд, AL10 9AB
Д. Б. Мунблит
Россия
Мунблит Даниил Борисович - PhD, профессор кафедры педиатрии и детских инфекционных болезней Первый МГМУ им. И.М. Сеченова; Почетный старший преподаватель Секции воспаления, регенерации и развития Национального института сердца и легких, Медицинский факультет, Имперский колледж Лондона.
Ул. Трубецкая, д. 8, стр. 2, Москва, 119991; Южный Кенсингтон, Лондон, SW7 2BU
Д. В. Бутнару
Россия
Бутнару Денис Викторович - кандидат медицинских наук, проректор по научной работе.
Ул. Трубецкая, д. 8, стр. 2, Москва, 119991
М. Ю. Надинская
Россия
Надинская Мария Юрьевна - кандидат медицинских наук, доцент кафедры пропедевтики внутренних болезней, гастроэнтерологии и гепатологии.
Ул. Трубецкая, д. 8, стр. 2, Москва, 119991
А. А. Заикин
Россия
Заикин Алексей Анатольевич - кандидат физико-математических наук, заместитель директора Центра анализа сложных систем Первый МГМУ им. И.М. Сеченова; профессор системной медицины Института женского здоровья и кафедры математики, Университетский колледж Лондона.
Ул. Трубецкая, д. 8, стр. 2, Москва, 119991; Гоуэр стрит, Лондон, WC1E 6BT






































